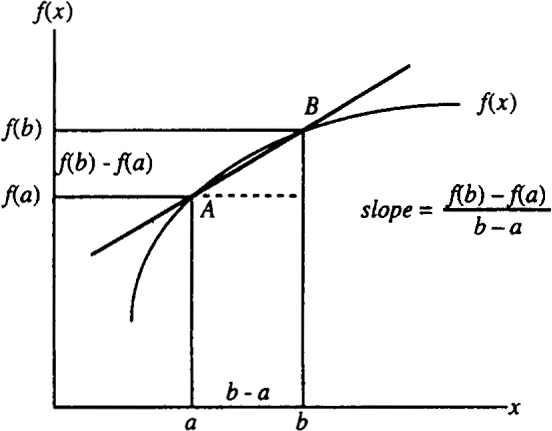
Fundamental Theorem of Calculus: \begin{align*} &\dfrac{d}{dx}\int f(t)dt=f(x)\\ &\int_a^b f(x)dx=F(b)-F(a) \end{align*}
|
|
| Class schedule by chapters/sections | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Functions, Graphs, and Models | Chapter R* Review R1-R3 Review R4-R7* | ||||||||||||
| Differentiation | 1.1-1.2 1.3-1.4,1.5(1) 1.5(2),1.6-1.7, 1.8* | ||||||||||||
| Exponential and Logarithm Functions |
2.1-2.4;
2.5*
| Exam 1 | Chap.R*, Chap.1-2
| Application of Differentiation
| 3.1-3.4* (max-min problems)
| Integration
| 4.1-4.3*, 4.4*-4.5*
| Exam 2 | Chap.3-4*
| Application of Integration** | 5.1-5.3*
| Cumulative Final Exam |
| |
| Notes from the Zoom | |||
|---|---|---|---|
| Week One | Chapter R*, Chapter 1 Z-hour board 1.1 board 1.2 | ||
| Week Two | Chapter 1, Chapter 2 board 2.1 board 2.2 board 2.3 | ||
| Week Three | Chapter 2, Chapter 3 board 3.1 board 3.2 board 3.3 board 3.4 | ||
| Review | Exam | Date |
|---|---|---|
| Review Exam I | Exam I | |
| Review Exam II | Exam II | |
| Review Exam III | Reading Assignment* | |
| Review Final | Final Exam |
Digital Calc \(\otimes\) DE models compressible fluids
