Math 1441   (Dr. J. S. Zheng)


Office: Math-Phys 3306
Phone: (912)478 1338
E-mail: szheng@GeorgiaSouthern.edu





Instantaneous rate of change at \(x=a\) equals to \(f'(a)=\lim_{h\to 0} \frac{f(a +h)-f(a)}{h}\)


Limit formulae: \( \lim_{x\to 0} \frac{\sin x}{x}=1.\)      \(\lim_{x\to\infty} (1+\frac{a}{x})^x=e^a\)

Fundamental Theorem of Calculus: \begin{align*} &\dfrac{d}{dx}\int f(t)dt=f(x)\\ &\int_a^b f(x)dx=F(b)-F(a) \end{align*}

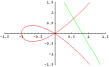
Generalized Witch of Agnesi paradox: Let \(y=\frac{1}{(1+x)^a} \),  \(0.5 < a \leqslant 1\),   \(x\in [0,\infty)\).
Then the volume of the solid of rovolution about the curve's asymptote is given by \(V=\pi\int_0^\infty \frac{1}{(1+x)^{2a}}dx=\frac{\pi}{2a-1}\) but the surface area of the solid of revolution is \begin{align*} &S=2\pi\int_0^\infty y \sqrt{1+y'^2} dx=\infty! \end{align*}

Interactive Integration
Taylor expansions
   
    		What Calculus can do

GSU Undergraduate Student Research
COSM UNDERGRAD RESEARCH OPPORTUNITIES
NASA STEM


Revised Schedule 03/30-05/01   Online Learning Resources  (ASC  Folio)

Schedule of the class
Class schedule by chapters/sections (tentative)
Functions (Review)1.1-1.6 
Limits and Continuity 2.1-2.2  2.3*   2.4-2.6
Differentiation 3.1-3.2  3.3, 3.5-3.6  3.7*-3.9*
Exam 1   Chap.2 and Chap.3
Applications of Derivatives 4.1  4.2-4.4  4.5-4.8
Exam 2   Chap.4
Integration 5.1  5.2  5.3-5.6 
Midterm 3   Chap.5
Applications of Definite Integrals 6.1 - 6.7
Cumulative Final Exam May 5, 12:30-2:30



Homework assignments   MyMathLab (ask Instructor for course code)  

The implicit function \(y=y(x)\) is defined by the equation    \( y^4-4y^2=x^4-9x^2\)



 


Office hours    Tuesday and Thursday 2:30-4:00 or by appointment


Test schedule following syllabus (tentative)
Review   Exam     Date  
Review Exam I    Exam I
Review Exam II Exam II
Review Exam III    Exam III  
Review Final      Final Exam                     


Math Tutoring   Academic Success Center


USG  Learning 

Computing Lab